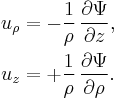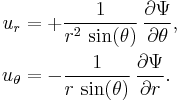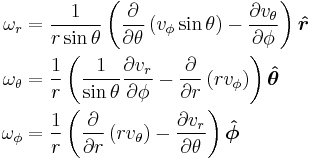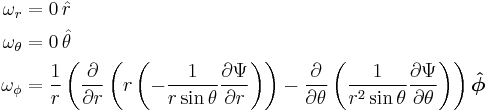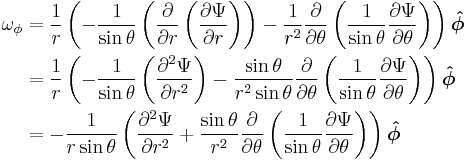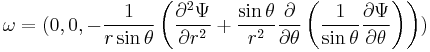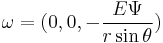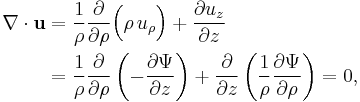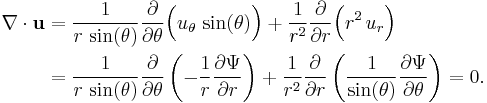Stokes stream function

For two-dimensional flows, see Stream function.

In fluid dynamics, the Stokes stream function is used to describe the streamlines and flow velocity in a three-dimensional incompressible flow with axisymmetry. A surface with a constant value of the Stokes stream function encloses a streamtube, everywhere tangential to the flow velocity vectors. Further, the volume flux within this streamtube is constant, and all the streamlines of the flow are located on this surface. The velocity field associated with the Stokes stream function is solenoidal—it has zero divergence. This stream function is named in honor of George Gabriel Stokes.

1 Cylindrical coordinates
2 Spherical coordinates
- 2.1 Vorticity
- 2.2 Comparison with cylindrical
3 Zero divergence
4 References
5 Notes

Cylindrical coordinates

Consider a cylindrical coordinate system ( ρ , φ , z ), with the z–axis the line around which the incompressible flow is axisymmetrical, φ the azimuthal angle and ρ the distance to the z–axis. Then the flow velocity components u_ρ and u_z can be expressed in terms of the Stokes stream function 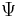$\Psi$ by:^[1]

$\begin{align} u_\rho &= - \frac{1}{\rho}\, \frac{\partial \Psi}{\partial z}, \\ u_z &= %2B \frac{1}{\rho}\, \frac{\partial \Psi}{\partial \rho}. \end{align}$

The azimuthal velocity component u_φ does not depend on the stream function. Due to the axisymmetry, all three velocity components ( u_ρ , u_φ , u_z ) only depend on ρ and z and not on the azimuth φ.

The volume flux, through the surface bounded by a constant value ψ of the Stokes stream function, is equal to 2π ψ.

Spherical coordinates

In spherical coordinates ( r , θ , φ ), r is the radial distance from the origin, θ is the zenith angle and φ is the azimuthal angle. In axisymmetric flow, with θ = 0 the rotational symmetry axis, the quantities describing the flow are again independent of the azimuth φ. The flow velocity components u_r and u_θ are related to the Stokes stream function 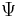$\Psi$ through:^[2]

$\begin{align} u_r &= %2B \frac{1}{r^2\, \sin(\theta)}\, \frac{\partial \Psi}{\partial \theta}, \\ u_\theta &= - \frac{1}{r\, \sin(\theta)}\, \frac{\partial \Psi}{\partial r}. \end{align}$

Again, the azimuthal velocity component u_φ is not a function of the Stokes stream function ψ. The volume flux through a stream tube, bounded by a surface of constant ψ, equals 2π ψ, as before.

Vorticity

See also: Stream_function#Vorticity

The vorticity is defined as:

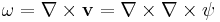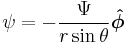$\mathbf{\omega} = \nabla \times \mathbf{v} = \nabla \times \nabla \times \mathbf{\psi}$ , where $\psi=-\frac{\Psi}{r\sin\theta}\boldsymbol{\hat \phi}$ .

Derivation of vorticity $\omega$ using a Stokes stream function

Consider the vorticity as defined by

$\mathbf{\omega} = \nabla \times \mathbf{v}$

From the definition of the curl in spherical coordinates:

$\begin{align} \omega_r &= {1 \over r\sin\theta}\left({\partial \over \partial \theta} \left( v_\phi\sin\theta \right) - {\partial v_\theta \over \partial \phi}\right) \boldsymbol{\hat r} \\ \omega_\theta &= {1 \over r}\left({1 \over \sin\theta}{\partial v_r \over \partial \phi} - {\partial \over \partial r} \left( r v_\phi \right) \right) \boldsymbol{\hat \theta} \\ \omega_\phi &= {1 \over r}\left({\partial \over \partial r} \left( r v_\theta \right) - {\partial v_r \over \partial \theta}\right) \boldsymbol{\hat \phi} \\ \end{align}$

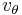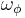First we notice that the $r$ and $\theta$ components are equal to 0. Secondly we substitute $v_r$ and $v_\theta$ into $\omega_\phi$ then we get:

$\begin{align} \omega_r &= 0\,{\hat r} \\ \omega_\theta &= 0\,{\hat \theta} \\ \omega_\phi &= {1 \over r}\left({\partial \over \partial r} \left( r \left(-\frac{1}{r \sin\theta}\frac{\partial\Psi}{\partial r}\right) \right) - {\partial \over \partial \theta}\left(\frac{1}{r^2 \sin\theta}\frac{\partial\Psi}{\partial \theta}\right)\right) \boldsymbol{\hat \phi} \\ \end{align}$

If we do the algebra:

$\begin{align} \omega_\phi &= {1 \over r}\left(-\frac{1}{\sin\theta}\left({\partial \over \partial r} \left(\frac{\partial\Psi}{\partial r}\right)\right) - \frac{1}{r^2 }{\partial \over \partial \theta}\left(\frac{1}{\sin\theta}\frac{\partial\Psi}{\partial \theta}\right)\right) \boldsymbol{\hat \phi} \\ &= {1 \over r}\left(-\frac{1}{\sin\theta}\left(\frac{\partial^2\Psi}{\partial r^2}\right) - \frac{\sin\theta}{r^2 \sin\theta}{\partial \over \partial \theta}\left(\frac{1}{\sin\theta}\frac{\partial\Psi}{\partial \theta}\right)\right) \boldsymbol{\hat \phi} \\ &= -\frac{1}{r\sin\theta} \left(\frac{\partial^2\Psi}{\partial r^2} %2B \frac{\sin\theta}{r^2}{\partial \over \partial \theta}\left(\frac{1}{\sin\theta}\frac{\partial\Psi}{\partial \theta}\right)\right) \boldsymbol{\hat \phi} \\ \end{align}$

If we do the calculation we find that the vorticity vector is equal to:

$\mathbf{\omega} = (0,0, -\frac{1}{r\sin\theta} \left(\frac{\partial^2\Psi}{\partial r^2} %2B \frac{\sin\theta}{r^2}{\partial \over \partial \theta}\left(\frac{1}{\sin\theta}\frac{\partial\Psi}{\partial \theta}\right)\right))$

If we define the new operator 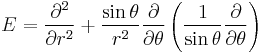$E = \frac{\partial^2}{\partial r^2} %2B \frac{\sin\theta}{r^2}{\partial \over \partial \theta}\left(\frac{1}{\sin\theta}\frac{\partial}{\partial \theta}\right)$ then we have

$\mathbf{\omega} = (0,0, -\frac{E\Psi}{r\sin\theta})$

Comparison with cylindrical

The cylindrical and spherical coordinate systems are related through

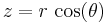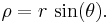
$z = r\, \cos(\theta)\,$ and $\rho = r\, \sin(\theta).\,$

Zero divergence

In cylindrical coordinates, the divergence of the velocity field u becomes:^[3]

$\begin{align} \nabla \cdot \mathbf{u} &= \frac{1}{\rho} \frac{\partial}{\partial \rho}\Bigl( \rho\, u_\rho \Bigr) %2B \frac{\partial u_z}{\partial z} \\ &= \frac{1}{\rho} \frac{\partial}{\partial \rho} \left( - \frac{\partial \Psi}{\partial z} \right) %2B \frac{\partial}{\partial z} \left( \frac{1}{\rho} \frac{\partial \Psi}{\partial \rho} \right) = 0, \end{align}$

as expected for an incompressible flow.

And in spherical coordinates:^[4]

$\begin{align} \nabla \cdot \mathbf{u} &= \frac{1}{r\, \sin(\theta)} \frac{\partial}{\partial \theta}\Bigl( u_\theta\, \sin(\theta) \Bigr) %2B \frac{1}{r^2} \frac{\partial}{\partial r}\Bigl( r^2\, u_r \Bigr) \\ &= \frac{1}{r\, \sin(\theta)} \frac{\partial}{\partial \theta} \left( - \frac{1}{r} \frac{\partial \Psi}{\partial r} \right) %2B \frac{1}{r^2} \frac{\partial}{\partial r} \left( \frac{1}{\sin(\theta)} \frac{\partial \Psi}{\partial \theta} \right) = 0. \end{align}$

References

Batchelor, G.K. (1967). An Introduction to Fluid Dynamics. Cambridge University Press. ISBN 0521663962.
Lamb, H. (1994). Hydrodynamics (6th ed.). Cambridge University Press. ISBN 9780521458689. Originally published in 1879, the 6th extended edition appeared first in 1932.
Stokes, G.G. (1842). "On the steady motion of incompressible fluids". Transactions of the Cambridge Philosophical Society 7: 439–453.
Reprinted in: Stokes, G.G. (1880). Mathematical and Physical Papers, Volume I. Cambridge University Press. pp. 1–16. http://www.archive.org/details/mathphyspapers01stokrich.

Notes

^ Batchelor (1967), p. 78.
^ Batchelor (1967), p. 79.
^ Batchelor (1967), p. 602.
^ Batchelor (1967), p. 601.